\( \def\Phit{\tilde{\Phi}} \def\es{\epsilon_s} \def\ep{\epsilon_p} \def\emm{\epsilon_m} \def\ez{\epsilon_0} \def\rr{{\mathbf r}} \def\s{{\mathbf s}} \def\nn{{\mathbf n}} \def\EE{{\mathbf e}} \def\PP{{\mathbf p}} \def\DD{{\mathbf d}} \def\rhot{\tilde{\rho}} \def\n{\mathbf{n}} \def\ei{\epsilon_\infty} \def\J{{\mathbf J}} \def\E{{\mathbf E}} \def\parn[1]{\left(#1\right)} \def\del[1]{\partial{#1}} \def\sdiv{{\nabla\cdot}} \def\epm{\epsilon_m} \def\R{\mathbb{R}} \def\zz{{\mathbf z}} \)

Features of SMPBICS

Feature 1: Construct a SMPBIC solution, \(u\), by the solution decomposition formula

\[ \begin{equation}\label{solutionSplit} u(\rr)=G(\rr) + \Psi(\rr) + \Phit(\rr) \quad \quad \forall \rr\in \Omega, \end{equation}\tag{1} \]

where \(G(\rr) = \frac{\alpha}{4\pi\ep} \sum_{j=1}^{n_p}\frac{z_{j}}{| \rr-\rr_j |}\), \(\Psi\) is defined by the linear interface boundary value problem:

\[ \begin{equation}\label{Psi-channel} \left\{\begin{array}{lll} \Delta \Psi(\rr)=0, \qquad \rr\in D_{m}\cup D_p\cup D_s, & \\ \Psi(\s^-)=\Psi(\s^+), \quad \ep \frac{\partial \Psi(\s^-)}{\partial\nn_p(\s)}=\es \frac{\partial \Psi(\s^+)}{\partial\nn_p(\s)}+(\es-\ep)\frac{\partial G(\s)}{\partial \nn_p(\s)}, & \s\in\Gamma_p, \\ \Psi(\s^-)=\Psi(\s^+), \quad \emm \frac{\partial \Psi(\s^-)}{\partial\nn_m(\s)}=\es \frac{\partial \Psi(\s^+)}{\partial\nn_m(\s)} +(\es-\emm)\frac{\partial G(\s)}{\partial \nn_m(\s)} + \tau \sigma, & \s\in\Gamma_m, \\ \tag{2} \Psi(\s^-)=\Psi(\s^+), \quad \ep \frac{\partial \Psi(\s^-)}{\partial\nn_p(\s)}=\emm \frac{\partial \Psi(\s^+)}{\partial\nn_p(\s)} +(\emm-\ep)\frac{\partial G(\s)}{\partial \nn_p(\s)}, & \s\in\Gamma_{pm}, \\ \Psi(\s) ={g}(\s) -G(\s), & \s\in \Gamma_D, \\ \frac{\partial \Psi(\s)}{\partial\nn_b(\s)} = - \frac{\partial G(\s)}{\partial \nn_b(\s)}, & \s \in \Gamma_{N}, \end{array}\right. \end{equation} \]

and \(\Phit\) is defined by a nonlinear system consisting of the \(n\) nonlinear algebraic equations,

\begin{equation} \label{smpbeic-def_1} c_{i}(\rr) - {c}_{i}^b \left[1- \gamma \sum\limits_{j=1}^n v_j c_j(\rr) \right]^{\frac{ v_i}{v_0}} w_i(\rr) e^{-Z_{i} \Phit(\rr)} =0, \qquad \rr\in D_s,\; i=1,2,\ldots, n, \tag{3} \end{equation}

and the linear interface boundary value problem

\[ \begin{equation} \label{smpbeic-def} \left\{\begin{array}{ll} \Delta \Phit(\rr)=0, &\rr\in D_{m}\cup D_p,\\ \es\Delta \Phit(\rr) + \beta \sum\limits_{i=1}^n Z_{i} c_i(\rr) = 0, & \rr\in D_s,\\ \Phit(\s^+)= \Phit(\s^-), \quad \es \frac{\partial \Phit(\s^+)}{\partial\nn_p(\s)}=\ep \frac{\partial \Phit(\s^-)}{\partial\nn_p(\s)}, & \s\in\Gamma_p,\\ \Phit(\s^+)= \Phit(\s^-), \quad \es \frac{\partial \Phit(\s^+)}{\partial\nn_m(\s)}=\emm \frac{\partial \Phit(\s^-)}{\partial\nn_m(\s)}, & \s\in\Gamma_m, \tag{4} \\ \Phit(\s^-)=\Phit(\s^+), \quad \ep \frac{\partial \Phit(\s^-)}{\partial\nn_p(\s)}=\emm \frac{\partial \Phit(\s^+)}{\partial\nn_p(\s)}, & \s\in\Gamma_{pm}, \\ \Phit(\s) = 0, & \s \in \Gamma_D, \\ \frac{\partial \Phit(\s)}{\partial \nn_b(s)} = 0, & s\in \Gamma_N. \end{array}\right. \end{equation} \]

where \(w_i=e^{-Z_{i} [G(\rr) + \Psi(\rr)]}\), which has been calculated before computing \(\Phit\).

In Physics, \(G\), \(\Psi\), and \(\Phit\) are the three electrostatic potentials induced by the atomic charges of VDAC protein, the membrane surface charges and Dirichlet boundary and interfaces values, and the ionic charges in the solvent region \(D_s\), respectively. Since \(G\) collects all the singularity points of \(u\). \(\Psi\) and \(\Phit\) can be calculated numerically without involving any singularity difficulties. Consequently, the complexity of solving the SMPBIC model can be reduced sharply by the solution decomposition formula \((1)\).

In the uniform ion size case (i.e., we set \(v_i = \bar{v} \) with \(\bar{v}= \frac{1}{n} \sum_{j=1}^n v_j \) for \(i=1,2,\ldots, n\)), with (3), we then can derive an analytical expression of \(c_i\),

\[ \begin{equation} \label{c-selection} c_i(\rr) = \frac{c_i^b w_i(\rr) e^{-Z_{i} \Phit(\rr)} }{1 + \gamma \frac{\bar{v}^2}{v_0} \sum\limits_{j=1}^n c_j^b w_i(\rr) e^{-Z_{i} \Phit(\rr)} }, \quad \rr \in D_s, \quad i=1,2,\ldots, n. \tag{5} \end{equation} \]

Applying the above expressions to (4) we get the nonlinear interface boundary value problem

\[ \begin{equation} \label{Phit-channel} \left\{\begin{array}{cl} \Delta \Phit(\rr)=0, &\rr\in D_{m}\cup D_p,\\ \epsilon_s \Delta \Phit(\rr) + \beta \frac{ \sum\limits_{i=1}^{n}Z_{i} c_{i}^{b} w_i(\rr)e^{-Z_{i}\Phit(\rr)}}{1 + \gamma \frac{\bar{v}^2}{v_0} \sum\limits_{i=1}^n c_{i}^{b} w_i(\rr) e^{-Z_{i}\Phit(\rr)}} =0, & \rr \in D_{s}, \\ \Phit(\s^+)= \Phit(\s^-), \quad \es \frac{\partial \Phit(\s^+)}{\partial\nn_p(\s)}=\ep \frac{\partial \Phit(\s^-)}{\partial\nn_p(\s)}, & \s\in\Gamma_p,\\ \Phit(\s^+)= \Phit(\s^-), \quad \es \frac{\partial \Phit(\s^+)}{\partial\nn_m(\s)}=\emm \frac{\partial \Phit(\s^-)}{\partial\nn_m(\s)}, & \s\in\Gamma_m, \tag{6} \\ \Phit(\s^-)=\Phit(\s^+), \quad \ep \frac{\partial \Phit(\s^-)}{\partial\nn_p(\s)}=\emm \frac{\partial \Phit(\s^+)}{\partial\nn_p(\s)}, & \s\in\Gamma_{pm}, \\ \Phit(\s) = 0, & \s \in \Gamma_D, \\ \frac{\partial \Phit(\s)}{\partial \nn_b(s)} = 0, & s\in \Gamma_N. \end{array}\right. \end{equation} \]

Applying the above problem solution \(\Phit\) to (1), we obtain a solution, \(u\), of the uniform SMPBIC model. See reference 1 and 2 for more details.


Feature 2: Calculate a total solvation free energy, \(E\), in kilocalorie per mole (kcal/mol) by

\[ \begin{equation} \label{electrostatics-total} E = E_{es, D_p} + E_{es, D_s} + E_{id} + E_{ex} - E_0, \tag{7} \end{equation} \]

where \(E_{es, D_p}\) denotes the electrostatic free energy induced by the atomic charges from the protein domain \(D_p\), \(E_{es, D_s}\) the electrostatic free energy induced by the ionic charges from the solvent domain \(D_s\), \(E_{id}\) the ideal gas solvation free energy, \(E_{ex}\) the excess solvation free energy, and \(E_0\) a nonpolar energy to a \(E=0\) in the case without involving any charges. Solving the SMPBIC model numerically, we can get electrostatic potential functions, \(G, \Psi, \Phit\), and \(u\), and ionic concentration functions, \(c_i\) for \(i=1,2,\ldots, n\). We then can calculate these energies by the formulas

\[ E_{es, D_p} = \left\{\begin{array}{ll} \frac{\lambda}{2}\sum_{j=1}^{n_p} z_j\Phit(\rr_j) & \mbox{if the water reference state is selected}\\ \frac{\lambda}{2}\sum_{j=1}^{n_p} z_j \left[ \Psi(\rr_j) + \Phit(\rr_j) \right] & \mbox{if $u_{ref} = G$ in the vacuum reference state,} \tag{8} \end{array}\right. \] \[ E_{es, D_s} = \lambda \gamma \sum_{i=1}^n Z_i \int_{D_s }u c_{i} d\rr, \qquad E_{id} = \gamma \sum_{i=1}^n \int_{D_s } c_{i}\left( \ln \frac{c_{i}}{c_i^b} -1\right) d\mathbf{r}, \] \[ E_{ex} = \frac{1}{v_0}\int_{D_s } \left[1-\gamma \sum_{i=1}^n v_i c_i \right] \left[ \ln \left(1-\gamma \sum_{i=1}^n v_i c_i \right) -1 \right] d\mathbf{r}, \] \[ E_0 = \lambda ||D_s|| \left[ \gamma \sum_{i=1}^n c_{i}^0\left( \ln \frac{c_{i}^0}{c_i^b} -1\right) + \frac{1}{v_0} \big(1-\gamma \sum_{i=1}^n v_i c_i^0 \big) \big[ \ln \big(1-\gamma \sum_{i=1}^n v_i c_i^0 \big) -1\big] \right], \]

where \(\lambda=\frac{N_{A}k_B T}{4184}\), which makes energy units to be kcal/mol, \(v_0 = \min_{1\leq i\leq n} v_i\), \( ||D_s||\) denotes the volume of \(D_s\), \(\gamma = N_A 10^{-27}\), which is about \(6.022 \times 10^{-4}\), and \(\{c_i^0\}_{i=1}^n\) denotes a set of ionic concentration constants in the case \(u=0\).

In fact, when \(u=0\), the algebraic system (3) is simplified as

\[ \begin{equation} \label{ci0-eq} c_{i} = c_{i}^{b} \left[1- \gamma \sum\limits_{j=1}^n v_j c_j \right]^{\frac{ v_i}{v_0}}, \quad i=1,2,\ldots,n. \end{equation} \]

Solving the above system, we can obtain the ionic concentration constants \(\{c_i^0\}_{i=1}^n\) as required to calculate \(E_0\). Specifically, in the uniform size case, applying \(u=0\) to (5), we can get \(c_i^0\) in the expression

\[ \begin{equation} \label{c0-def-uniform} c_{i}^0 =\frac{ c_{i}^{b}}{1 + \gamma v_0 \sum\limits_{j=1}^n c_j^b}, \quad i=1,2,\ldots,n. \end{equation} \]

The excess energy \(E_{ex}\) reflects the work induced by the size constraint conditions (4) while \(E_{es, D_p}\) gives the energy required to move an ion channel protein from a reference state to the current state (the system in an ionic solution). Here two reference states are set by considering the protein in water and vacuum, resulting in two different reference potentials, \(u_{ref}=G+\Psi\) and \(u_{ref}=G\), respectively. See reference 3 for more information.


Feature 3: Visualize potential and ionic distribution profiles across the outer mitochondrial membrane by two dimensional curves. Here each curve is plotted by using the average values of ionic concentration functions \(c_i\) over a block partition of a solvent domain, \(D_s\), in the normal direction of the membrane. Such a figure (see Figure 1 as an example) make it easy for us to view the ionic distribution profiles and compare the ionic concentration functions generated by different models.

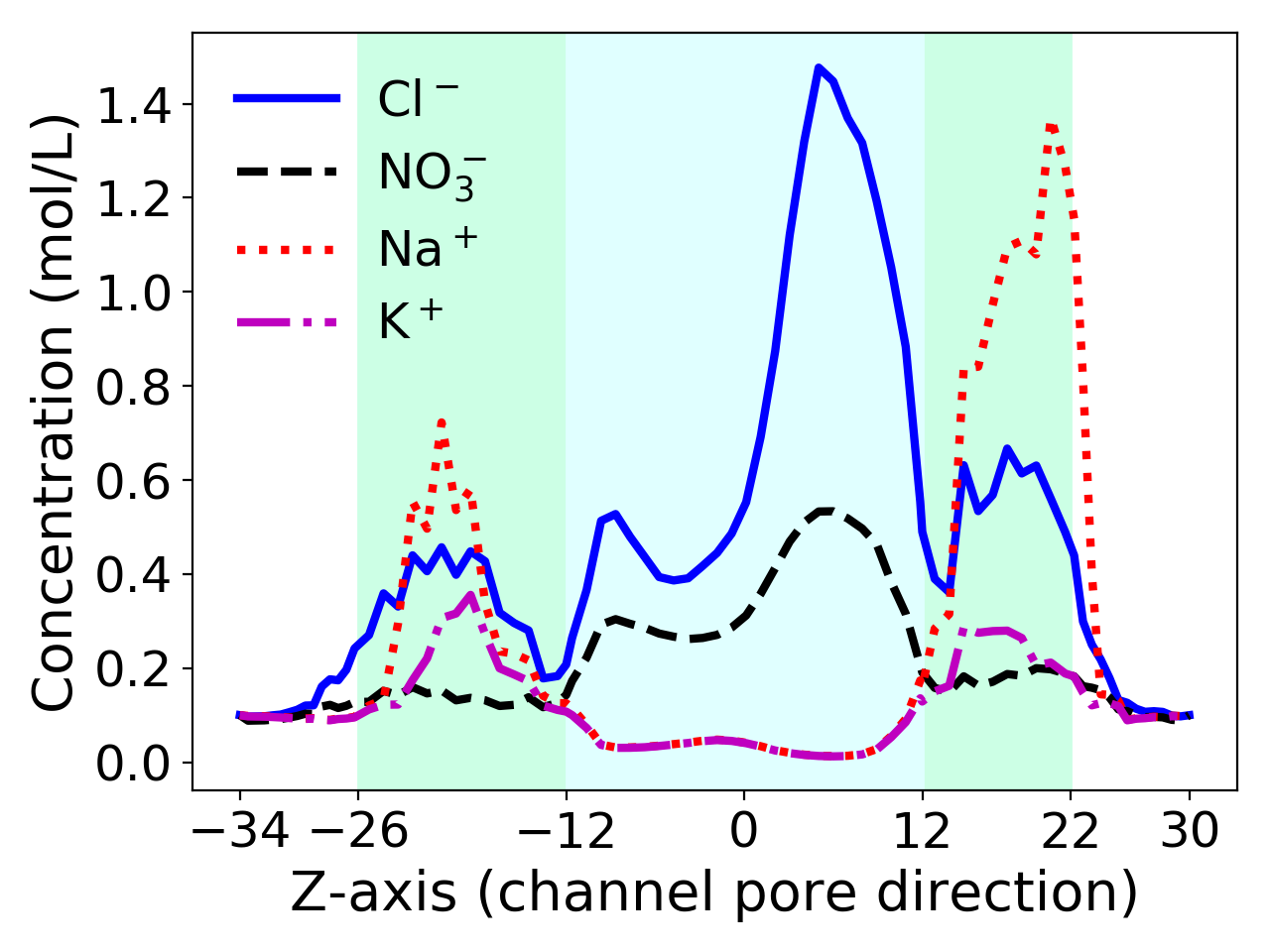
Nonuniform SMPBICS Model
(a) By the nonuniform SMPBIC model
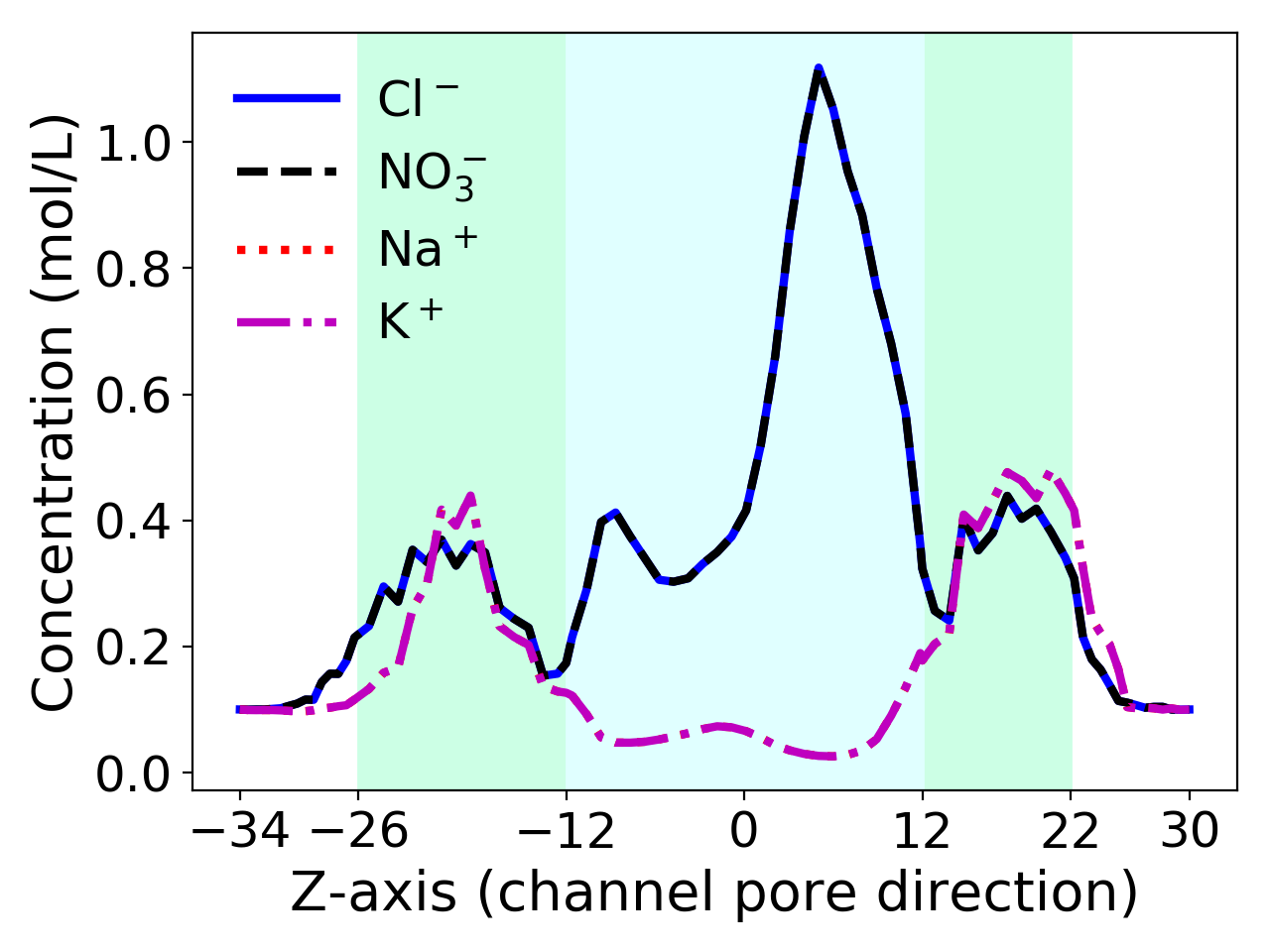
Uniform SMPBICS Model
(b) By the uniform SMPBIC model
Figure 1. A comparison of the ionic concentration functions \(c_i\) generated by the nonuniform SMPBIC model (i.e. the SMPBIC model with ionic species having nonuniform ionic sizes) with those by the uniform SMPBIC model for a VDAC ion channel protein (PDB ID: 3EMN) in a mixture of 0.1 molar KNO\(_3\) and 0.1 molar NaCl. Here the ion sizes \(v_i\) of the four ionic species Cl\(^-\), Na\(^+\), K\(^+\), and NO\(_3^-\) and their average volume \(\hat{v}\) are given as \(v_1= 24.8384, \quad v_2=77.0727, \quad v_3=9.8547, \quad v_4=3.5914, \quad \hat{v} = 28.8393\); the central part of the channel pore that links to the membrane (\(-12\leq z\leq 12\)) is highlighted in light-cyan; and the other parts of the channel pore are highlighted in green.

Figure 1 shows that the maximum concentration value of Cl\(^-\) is almost triple that of NO\(_3^-\) (1.48 vs. 0.53) simply because the size of a Cl\(^-\) ion is much smaller than that of a NO\(_3^-\) ion (24.84 vs. 77.07). For cations, the maximum concentration value of Na\(^+\) is almost four times that of K\(^+\) (1.37 vs. 0.36) in the range \(12 < z < 22\) highlighted in green since the size of a K\(^+\) ion is about triple that of a Na\(^+\) ion (9.85 vs. 3.59), demonstrating that the nonuniform SMPBIC model can well retain the anion selectivity property of VDAC, ionic sizes have significant impacts on electrostatics and ionic concentrations, and the anion selectivity happens mostly within the central part of the ion channel pore.

However, in the uniform ion size case, the 2D curves of concentrations of the two anion species Cl\(^-\) and NO\(_3^-\) and the two cation species K\(^+\) and Na\(^+\) are overlapped each other, respectively, implying that the concentrations of Cl\(^-\) and NO\(_3^-\) (or K\(^+\) and Na\(^+\)) are identical each other. This matches exactly what we could expect in physics when all the ions have the same size, the same charge number (\(-1\) for the anions Cl\(^-\) and NO\(_3^-\) and \(+1\) for the cations K\(^+\) and Na\(^+\)), and the same bulk concentration 0.1 mol/L. Even so, the uniform SMPBIC model is still Abel to well reflect the anion selectivity property of VDAC. Hence, it remains a valuable model in ion channel simulation and study due to its simplicity.

References

  1. D. Xie. An Efficient Finite Element Iterative Method for Solving a Nonuniform Size Modified Poisson-Boltzmann Ion Channel Model, Vol. 470, DOI 19.1016/j.jcp.2023.112043, Journal of Computational Physics, pages 111556: 1-15, 2023.
  2. D. Xie, S.H. Audi, and R.K. Dash. A Size Modified Poisson-Boltzmann Ion Channel Model in a Solvent of Multiple Ionic Species: Application to VDAC, Journal of Computational Chemistry, Vol. 41 (3), pages 218-231, 2020.
  3. Liam Jemison, Matthew Stahl, Ranjan K. Dash, and Dexuan Xie. VDAC Solvation Free Energy Calculation by a Nonuniform Size Modified Poisson-Boltzmann Ion Channel Model. arXiv:2407.01569v1 May 2024.