Welcome to the SMPBS Web Server (Updated 04/05/2024)

SMPBS (Size Modified Poisson-Boltzmann Solvers) is a comprehensive library of solvers for the size modified Poisson-Boltzmann equation (SMPBE). This library integrates various computational techniques, such as finite element, finite difference, solution decomposition, domain decomposition, and multigrid methods. SMPBS has been recognized in the prestigious the Journal of Computational Chemistry [3]. In this updated version, SMPBS has been extended to work for a biomolecule in an ionic solution with multiple species and distinct ionic sizes. It also includes the classic Poisson-Boltzmann equation (PBE) as an extension of a related platform known as the the SDPBS web server. Together, these resources form a robust toolkit for biochemists, biophysicists, bioengineers, and medical scientists for tackling a wide range of computational chemistry, computational biology, and molecular modeling problems

\( \def\Phit{\tilde{\Phi}} \def\es{\epsilon_s} \def\ep{\epsilon_p} \def\ez{\epsilon_0} \def\rr{{\mathbf r}} \def\s{{\mathbf s}} \def\nn{{\mathbf n}} \def\EE{{\mathbf e}} \def\PP{{\mathbf p}} \def\DD{{\mathbf d}} \def\rhot{\tilde{\rho}} \def\n{\mathbf{n}} \def\ei{\epsilon_\infty} \)

Applications of the SMPBS Web Server

The SMPBS web server serves as a platform for computing the electrostatic solvation energy of a biomolecule. To get started, click the link below. Please ensure that Javascript is enabled in your browser to access the SMPBS web server's user-friendly interface.

Calculate the electrostatic solvation energy of a biomolecule

The SMPBE Model

In the SMPBS web server, the electrostatics of a biomolecule in an ionic solution with \( n \) species is calculated by solving a nonuniform size modified Poisson-Boltzmann equation (nuSMPBE), a uniform SMPBE (uSMPBE), or a Poisson-Boltzmann equation. In particular, nuSMPBE is defined as a nonlinear system that consists of the \( n \) nonlinear algebraic equations,

\[ c_i(\mathbf{r}) - c_i^b \left[ 1 - \gamma \sum_{j=1}^n v_j c_j(\mathbf{r}) \right]^{\frac{v_i}{v_0}} e^{-Z_i u(\mathbf{r})} = 0, \quad \mathbf{r} \in D_s, \quad i = 1, 2, \ldots, n, \tag{1} \label{eq1} \] the two Poisson equations, \[ - \epsilon_p \Delta u(\mathbf{r}) = \alpha \sum_{j=1}^{n_p} Z_j \delta_{\mathbf{r}_j}, \quad \mathbf{r} \in D_p , \\ - \epsilon_s \Delta u(\mathbf{r}) = \beta \sum_{i=1}^n Z_i c_i(\mathbf{r}), \quad \mathbf{r} \in D_s, \tag{2} \label{eq2} \] the interface conditions \[ u(\mathbf{s}^-) = u(\mathbf{s}^+), \quad \epsilon_p \frac{\partial u(\mathbf{s}^-)}{\partial \mathbf{n}_p(\mathbf{s})} = \epsilon_s \frac{\partial u(\mathbf{s}^+)}{\partial \mathbf{n}_p(\mathbf{s})}, \quad \mathbf{s} \in \Gamma, \] and the Dirichlet boundary value condition \[ u(\mathbf{s}) = g(\mathbf{s}), \quad \mathbf{s} \in \partial \Omega, \]

where ∂Ω denotes the boundary of a sufficiently large bounded domain Ω , Dp, Ds, and Γ denote a protein region, a solvent region, and an interface between the protein and solvent regions, respectively, which satisfy that Ω = Dp ∪ Ds ∪ Γ as illustrated in Figure 1. The other parameters are given in Tables 1,2, and 3.

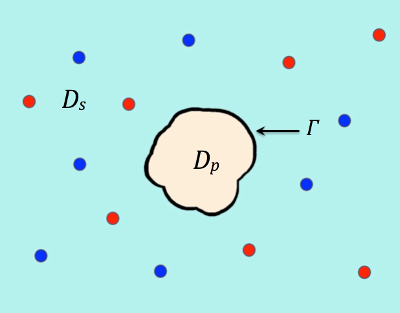
Protein region illustration

Figure 1. An illustration of a protein region Dp surrounded by solvent region Ds.
Γ denotes the interface and the two species of ions are colored in red and blue.

As a special case, when \( v_i = \overline{v} \) for \( i = 1,2,\ldots,n \) with \( \overline{v} = \frac{1}{n} \sum_{j=1}^{n} v_j \), from the size constraint equations of (1), we can get an analytical expression of \( c_i \), \[ c_i(\mathbf{r}) = \frac{c_i^b e^{-Z_i u(\mathbf{r})}}{1 + \gamma \frac{\overline{v}^2}{v_0} \sum_{j=1}^n c_j^b e^{-Z_j u(\mathbf{r})}}, \quad i = 1, 2, \ldots, n. \] Applying the above expressions to Eq. (2), we can reduce nuSMPBE to uSMPBE as follows: \[ \left\{ \begin{array}{cl} - \epsilon_p \Delta u(\mathbf{r}) = \alpha \sum_{j=1}^{n_p} Z_j \delta_{\mathbf{r}_j}, & \mathbf{r} \in D_p, \\ \epsilon_s \Delta u(\mathbf{r}) + \beta \frac{\sum_{i=1}^n Z_i c_i^b e^{-Z_i u(\mathbf{r})}}{1 + \gamma \frac{\overline{v}^2}{v_0} \sum_{i=1}^n c_i^b e^{-Z_i u(\mathbf{r})}} = 0, & \mathbf{r} \in D_s, \\ u(\mathbf{s}^-) = u(\mathbf{s}^+), \quad \epsilon_p \frac{\partial u(\mathbf{s}^+)}{\partial \mathbf{n}_p(\mathbf{s})} = \epsilon_s \frac{\partial u(\mathbf{s}^-)}{\partial \mathbf{n}_p(\mathbf{s})}, & \mathbf{s} \in \Gamma, \\ u(\mathbf{s}) = g(\mathbf{s}), & \mathbf{s} \in \partial \Omega. \end{array} \right. \]

When none of ionic size effects are considered (i.e. set all vi = 0), uSMPBE is reduced to PBE as follows: \begin{equation*} \label{PBEic} \left\{\begin{array}{cl} - \epsilon_p\Delta u(\rr) =\alpha \sum\limits_{j=1}^{n_{p}}z_{j} \delta_{\rr_{j}}, & \rr \in D_{p}, \\ \epsilon_s \Delta u(\rr) + \beta \sum\limits_{i=1}^{n}Z_{i} c_{i}^{b}e^{-Z_{i}u(\rr)} =0, & \rr \in D_{s}, \\ u(\s^-) = u(\s^+), \quad \ep \frac{\partial u(\s^+)}{\partial \nn_p(\s)} = \es \frac{\partial u(\s^-)}{\partial \nn_p(\s)}, & \s\in\Gamma,\\ u(\s) ={g}(\s), &\s\in \partial \Omega. \end{array} \right. \end{equation*}

Additional Notation

Table 1. Physical constants of SMPBE.
Parameter Value Unit (abbr.) Description
ε0 8.854187817 × 10-12 Farad/meter (F/m) Permittivity of vacuum
ec 1.602176565 × 10-19 Coulomb (C) Elementary charge
kB 1.380648813 × 10-23 Joule/Kelvin (J/K) Boltzmann constant
NA 6.0221409 × 1023 Mole-1 (mol-1) Avogadro constant

Table 2. SMPBE model parameters.
Parameter Default Value Unit (abbr.) Description
Λ 3.11 Angstrom (Å) Uniform ionic size parameter
εp 2.0 Unitless Biomolecular region dielectric constant
εs 80.0 Unitless Solvent region dielectric constant
T 298.15 Kelvin (K) Absolute temperature
Is 0.1 Mole/Liter (mol/l) Ionic strength

Table 3. Other SMPBE notation.
Parameter Description
Dp Protein region
Ds Solvent region
Γ Interface between Dp and Ds
Ω Computational domain satisfying Ω = Dp ∪ Ds ∪ Γ
∂Ω Boundary of Ω
rj Position of atom j (in angstroms)
zj Charge number of atom j
n(s) Unit outward normal vector of Dp
g Boundary value function
δrj Dirac-delta distribution at atomic position rj

The SMPBE Solver and Program Package

The SMPBE model is solved numerically in the SMPBS web server by a finite element solver developed in Prof. Dexuan Xie's research group. The computer programs are written in C++, C, Fortran, and Python based on the state-of-the-art finite element library DOLFIN from the FEniCS Project [1]. Their finite element meshes are generated by our molecular surface-fitted tetrahedral mesh generator [2], which uses the molecular triangulation surface mesh generated from TMSmesh. [4]

Using the SMPBS Web Server

You can simply input a protein PDB ID and let the SMPBS web server generate the PQR file. You can also generate a PQR file by downloading a PDB file of the biomolecule from the RCSB Protein Data Bank (PDB), and then converting it to a PQR file by using the web server PDB2PQR. Next, adjust calculation parameters as desired, and submit the job. A typical work flow for a job submission in calculating solvation energy is illustrated in Figure 2.

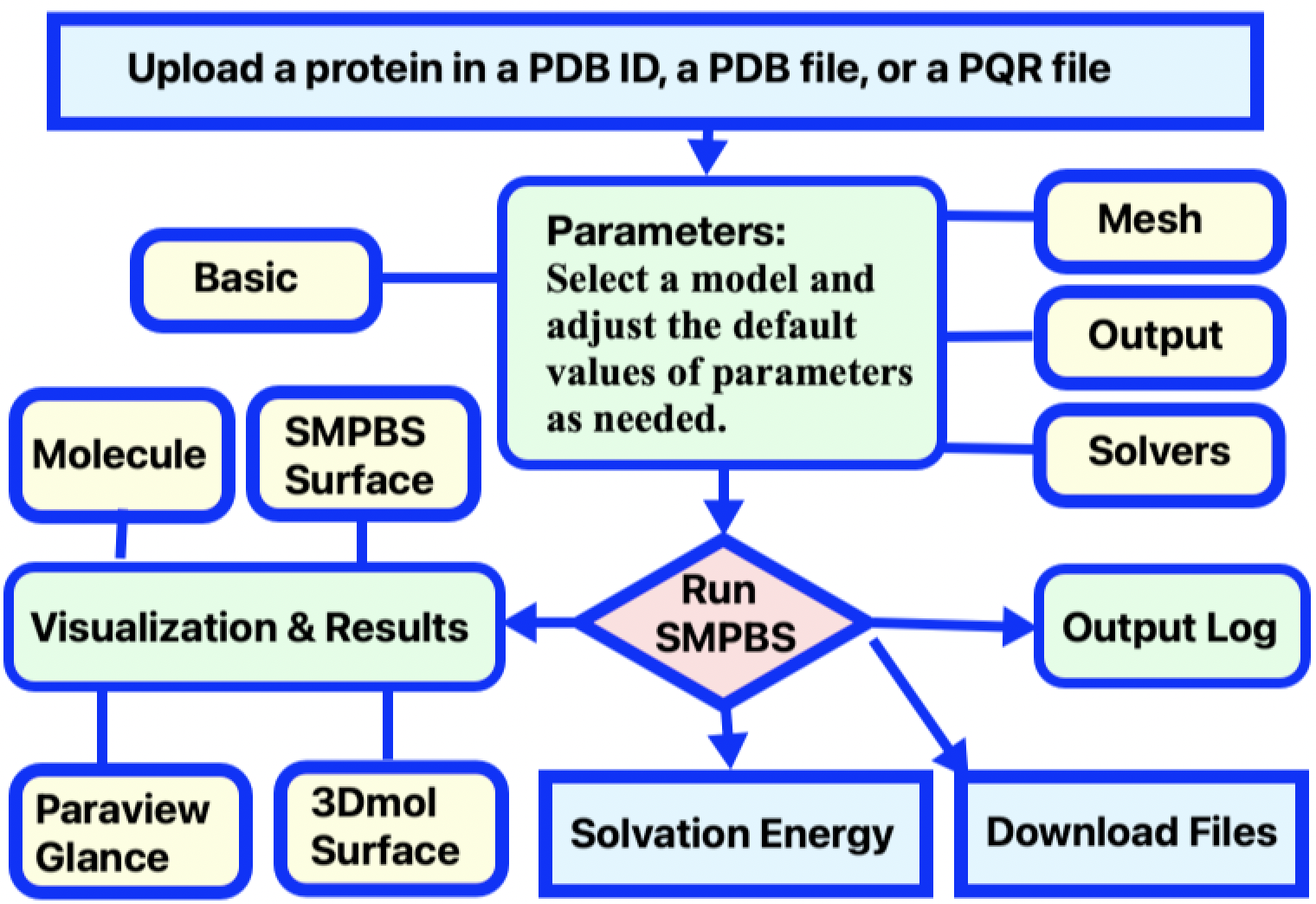
User workflow diagram

Figure 2. Diagram of of SMPBS Solvation Energy user workflow.

Credits

The SMPBS web server is developed by Professor Dexuan Xie's research group in the Department of Mathematical Sciences at University of Wisconsin-Milwaukee (UWM). It is hosted and maintained by the Information Technology Office in the College of Letters and Science at UWM. Development is partially supported by the National Science Foundation, USA, through grant DMS-1226259 and DMS-2153376. Please contact Dexuan Xie via email (dxie@uwm.edu) with any questions regarding the server.

Citing

If this web server is useful in your work, please use the following citation:

  • Yang Xie, J. Ying, and D. Xie. SMPBS: Web server for computing biomolecular electrostatics using finite element solvers of size modified Poisson-Boltzmann equation, Journal of Computational Chemistry, 38 (8) (2017) 541-552.

Additional Acknowledgements

  • Max Anthony Dreher and Andrew Ly - implementation of the updated SMPBS web server.
  • Jeremy Streich - initial implementation of SDPBS web server and socket programming
  • UWM L&S IT Office - internal web development framework and libraries
  • Professor David Koes - guidance on integrating 3Dmol.js [5]
  • Drs. Yi Jiang and Jinyong Ying - help with SMPBE solver libraries

Update History

  • 05/15/2024 - Updated the SMPBS web sever for an ionic solution with multiple species.
  • 04/05/2024 - Binding case and pKa temporarily removed.
  • 09/10/2023 - Paraview Glance.
  • 08/30/2023 - Updated the mesh generation package by using TMSmesh.
  • 08/30/2023 - Remove the solvent-excluded surface (SES) and the solvent-accessible surface (SAS) to simplify the usage.
  • 08/30/2023 - Remove the hybrid solver to simplify the usage.
  • 08/03/2023 - Updated home page.
  • 12/05/2017 - Add reference [3].
  • 10/25/2016 - Initial release.

References

  1. A. Logg, K.-A. Mardal, and G. N. Wells, eds., Automated Solution of Differential Equations by the Finite Element Method, vol. 84 of Lecture Notes in Computational Science and Engineering, Springer Verlag, 2012. [PDF]
  2. Liam Jemison, Matthew Stahl, Ranjan K. Dash, and Dexuan Xie. VDAC Solvation Free Energy Calculation by a Nonuniform Size Modified Poisson-Boltzmann Ion Channel Model. arXiv:2407.01569v1 May 2024.
  3. Yang Xie, J. Ying, and D. Xie. VDAC Solvation Free Energy Calculation by a Nonuniform Size Modified Poisson-Boltzmann Ion Channel Model , Journal of Computational Chemistry, 38 (8) (2017) 541-552. [PDF]
  4. M. Chen, B. Tu, B. Lu, Triangulated manifold meshing method preserving molecular surface topology, Journal of Molecular Graphics and Modelling 38 (2012) 411-418.
  5. Nicholas Rego and David Koes. 3Dmol.js: molecular visualization with WebGL. Bioinformatics 31 (8) (2015) 1322-1324 doi:10.1093/bioinformatics/btu829. [PDF]